70. 爬楼梯
题目:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
解答:
- 方法一:自己想的

时间复杂度:O(n),空间复杂度:xx
主要逻辑:以 2 的个数作为概率计算的循环,引用了阶乘处理方法
参考函数如右概率计算公式 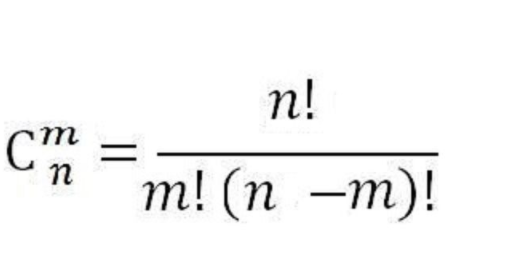
var climbStairs = function(n) {
let twoNum = Math.floor(n / 2); // 最多有 twoNum 个 2
let oneNum = n % 2;// 最多有 oneNum 个 2
// 以 2 的个数作为次数累计
let times = 0; // 0 个 2 -- 记一次
for(let i = 0; i <= twoNum; i++) {
// 处理阶乘
function factorialize(num) {
if(num == 0){
return 1;
}
return num * factorialize(num-1);
}
// 处理全是 1 或者全是2 - 偶数
if (i === 0 || (i === twoNum && oneNum === 0)) {
times += 1;
continue
}
// 或者全是2,一个1 - 奇数
if (i === twoNum && oneNum === 1) {
times += twoNum + 1;
continue
}
let top = i; // 2 的个数
let bottom = ((twoNum - i) * 2 + oneNum) + i; // 总的 2 和 1 的个数
// 概率
let plus = factorialize(bottom) / (factorialize(top) * factorialize(bottom - top));
times += plus;
}
return times;
};
- 方法二:动态规划
核心逻辑:将问题拆分成多个子问题 —> 爬第n阶楼梯的方法数量,等于 2 部分之和
- 爬上
n - 1阶楼梯的方法数量。因为再爬 1 阶就能到第 n 阶 - 爬上
n - 2阶楼梯的方法数量,因为再爬 2 阶就能到第 n 阶
分析完逻辑可以发现 —> 这已经是 斐波那契数 的算法问题了
// 贴一下官方提供的动态规划解法 -- 你猜我看懂了么?
var climbStairs = function(n) {
let p = 0, q = 0, r = 1;
for (let i = 1; i <= n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
};