113. 路径总和 II/二叉树中和为目标值的路径
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
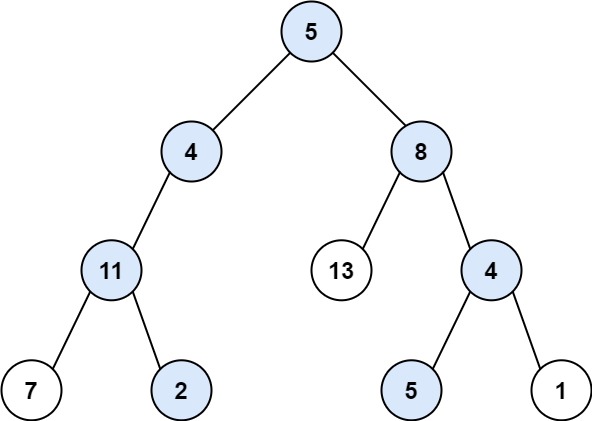
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
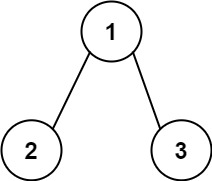
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
- 之前学习回溯算法时,这道题作为例题看过
套用回溯算法的思路
设定一个结果数组result来存储所有符合条件的路径
设定一个栈stack来存储当前路径中的节点
设定一个和sum来标识当前路径之和
- 从根结点开始深度优先遍历,每经过一个节点,将节点入栈
- 到达叶子节点,且当前路径之和等于给定目标值,则找到一个可行的解决方案,将其加入结果数组
- 遍历到二叉树的某个节点时有2个可能的选项,选择前往左子树或右子树
- 若存在左子树,继续向左子树递归
- 若存在右子树,继续向右子树递归
- 若上述条件均不满足,或已经遍历过,将当前节点出栈,向上回溯
var pathSum = function(root, targetSum) {
let result = []; // 存储结果
if(root) {
FindPath(root, targetSum, [], 0, result)
}
return result;
function FindPath(node, target, stack, sum, result) {
stack.push(node.val); // 记录路径 - 栈stack
sum += node.val; // 路径之和
// 找到叶子节点
if(node.left === null && node.right === null && sum === target) {
result.push(stack.slice(0));
}
// 还没到叶子节点 - 左右子树
if(node.left){
FindPath(node.left, target, stack, sum, result)
}
if(node.right) {
FindPath(node.right, target, stack, sum, result)
}
stack.pop() // 如果已经到叶子节点,且不满足条件,那么路径往前倒一个
}
};
画图理解: