二叉树:前中后序、层序遍历-递归/非递归版本、层序遍历、路径和
class TreeNode { // 创建节点
constructor(value, left, right) {
this.val = value || 0;
this.left = left || null;
this.right = right || null; }
}
系统梳理二叉树常见遍历方式
分类方式1:按遍历顺序
- 深度优先搜索 DFS【访问根节点的时机不同】
- 前序遍历:根节点-左子树-右子树
- 中序遍历:左子树-根节点-右子树
- 后序遍历:左子树-右子树-根节点
- 广度优先搜索 BFS
- 层序遍历:借助【队列】实现(从上到下,从左到右访问节点)
分类方式2:按实现方式
- 递归:代码简洁,但可能栈溢出
- 非递归:使用【栈/队列】实现,适合大量数据
分类方式3:特殊遍历
- 左视图:获取每层第一个节点,在层序遍历上修改
- 路径和:回溯算法,一般通过递归实现
let insertLNode = (root, value) => { // 插入左侧,并返回
if(value){ root.left = new TreeNode(value); return root.left; }
}
let insertRNode = (root, value) => { // 插入右侧,并返回
if(value){ root.right = new TreeNode(value); return root.right; }
}
// 二叉树创建函数 - 方便调试
let createTree = function (nodes) {
let root = new TreeNode(nodes[0]); // 第一项为根节点
let result = [], i = 1;
result.push(root);
while (result.length !== 0) {
let node = result.shift();
if (node) {
if (i < nodes.length) {
result.push(insertLNode(node, nodes[i])); // 左节点
result.push(insertRNode(node, nodes[i + 1])); // 右节点
}
i += 2;
}
}
return root
}
const example = createTree([1, 2, 4, 23, null, 23, 45, 3, 124, 346, null, 1, 0, 90, null]);
一、中序遍历、前序遍历、后续遍历
1、递归实现
// 前序:根-左-右。遍历到这个节点就取值 123
function preOrder(root) {
if(!root) return [];
return [root.val, ...preOrder(root.left), ...preOrder(root.right)]
}
// 中序:左-根-右。先深入到左侧叶子节点再取值 213
function inOrder(root) {
if(!root) return [];
return [...inOrder(root.left), root.val, ...inOrder(root.right)]
}
// 后序:左-右-根。先左叶子后右叶子最后根节点 231
function postOrder(root) {
if(!root) return [];
return [...postOrder(root.left), ...postOrder(root.right), root.val]
}
2、非递归实现:借用栈实现
前序:根-左-右 123
function preOrder(root) {
if(!root) return [];
const result = [];
const stack = [root];
while(stack.length) {
const node = stack.pop(); // 尾部取出
result.push(node.val);
if(node.right) { stack.push(node.right) }
if(node.left) { stack.push(node.left) }
}
return result;
}
中序:左-根-右 213
function inOrder(root) {
const result = [];
const stack = [];
let current = root;
while(stack.length || current) {
while(current) {
stack.push(current);
current = current.left;
}
current = stack.pop();
result.push(current.val);
current = current.right;
}
return result
}
后序:左-右-根 231
function postOrder(root) {
if(!root) return [];
const result = [];
const stack = [root];
while(stack.length) {
const node = stack.pop();
result.unshift(node.val); // 和 前序遍历的差异1 从 pop 改为 unshift
if(node.left) { stack.push(node.left) }
if(node.right) { stack.push(node.right) } // 和 前序遍历的差异2 先左后右
}
return result;
}
二、层序遍历
- 基于队列的 BFS【推荐】
- 基于递归的 DFS
1、基于队列的 BFS
// 实现方式:BFS广度优先 + 队列
function levelOrder(root) {
if (!root) return [];
const queue = [root]; // 队列操作 shift + push
const result = [];
while (queue.length) {
const levelSize = queue.length;
const currentLevel = [];
for (let i = 0; i < levelSize; i++) {
const node = queue.shift();
currentLevel.push(node.val); // 当前层
if (node.left) queue.push(node.left);
if (node.right) queue.push(node.right);
}
result.push(currentLevel);
}
return result;
}
2、基于递归的 DFS - leetcode:102 题
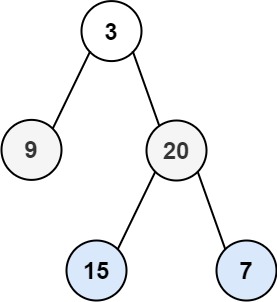
给你二叉树的根节点 root ,返回其节点值的 层序遍历。
// 示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
// 示例 2:
输入:root = [1]
输出:[[1]]
// 示例 3:
输入:root = []
输出:[]
// 实现方式:DFS深度优先搜索 + 递归
function levelOrder(root) {
const result = [];
if(root) {
FindLayer(root, result, 0);
}
return result;
function FindLayer(node, result, index) {
// 层级记录 - index 是层级
if(Array.isArray(result[index])) {
result[index].push(node.val);
} else {
result[index] = [node.val]
}
// 进入下一层
let currentIndex = index + 1;
if(node.left) {
FindLayer(node.left, result, currentIndex);
}
if(node.right) {
FindLayer(node.right, result, currentIndex);
}
}
};
三、特殊遍历:左视图
// 层次遍历基础上修改
function leftView(root) {
if (!root) return [];
let res = [];
let queue = [root];
while (queue.length) {
let len = queue.length;
for (let i = 0; i < len; i++) {
let node = queue.shift();
if (i === 0) { res.push(node.value) } // 记录每层的第一个节点
if (node.left) { queue.push(node.left) }
if (node.right) { queue.push(node.right) }
}
}
return res
}
四、特殊遍历:二叉树中和为目标值的路径
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
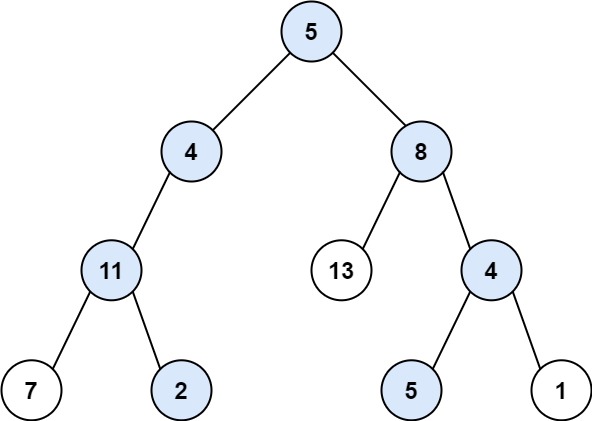
// 示例 1
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
// 示例 2:
输入:root = [1,2,3], targetSum = 5
输出:[]
// 示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
function pathSum(root, target) {
const result = [];
function backtrack(node, target, path) {
if (!node) return;
path.push(node.val);
if (!node.left && !node.right && target === node.val) {
result.push([...path]); // 走到叶子节点 + 找到一条路径
}
backtrack(node.left, target - node.val, path); // 递归左子树
backtrack(node.right, target - node.val, path); // 递归右子树
path.pop(); // 回溯
}
backtrack(root, target, []);
return result;
}